When to use Integration by Parts vs. U-Substitution
Deciding between integration by parts and u-substitution comes down to recognizing specific patterns in the integral.
For the integral , the correct method is integration by parts.
Here’s a breakdown of how to make that decision.
Key Differences and When to Use Each Method
U-Substitution
The goal of u-substitution is to simplify the integral into a much more basic form, like or .
Look for: A function and its derivative (or a constant multiple of its derivative) present in the integral.
- Classic Example: In , you can see the function and its derivative . This is a perfect candidate for substitution where .
In your problem, , the derivative of is , which isn't present. The derivative of is , which doesn't help simplify the logarithm. Therefore, substitution is not the best first step.
Integration by Parts
This method is specifically designed to solve integrals that are a product of two unrelated functions. The formula is .
Look for: A product of two different function types, such as:
- An algebraic function and a logarithmic function (like your problem)
- An algebraic function and an exponential function (e.g., )
- An algebraic function and a trigonometric function (e.g., )
Your integral is a textbook example of this pattern—it's the product of an algebraic function () and a logarithmic function ().
How to Apply Integration by Parts to Your Problem
To choose which part is '' and which is '', a helpful mnemonic is LIATE:
- Logarithmic
- Inverse Trigonometric
- Algebraic
- Trigonometric
- Exponential
Choose your '' based on whichever function type appears first in the LIATE list.
-
Identify the function types:
- is Logarithmic.
- is Algebraic.
-
Choose u: Since 'L' comes before 'A' in LIATE, we choose:
-
Differentiate u and integrate dv:
-
Apply the formula: The new integral, , is now a rational function that can be solved with algebraic manipulation (like polynomial long division) and is simpler than the original problem.
Introducing terms
This technique involves introducing a "1" term into the integral to facilitate integration by parts.
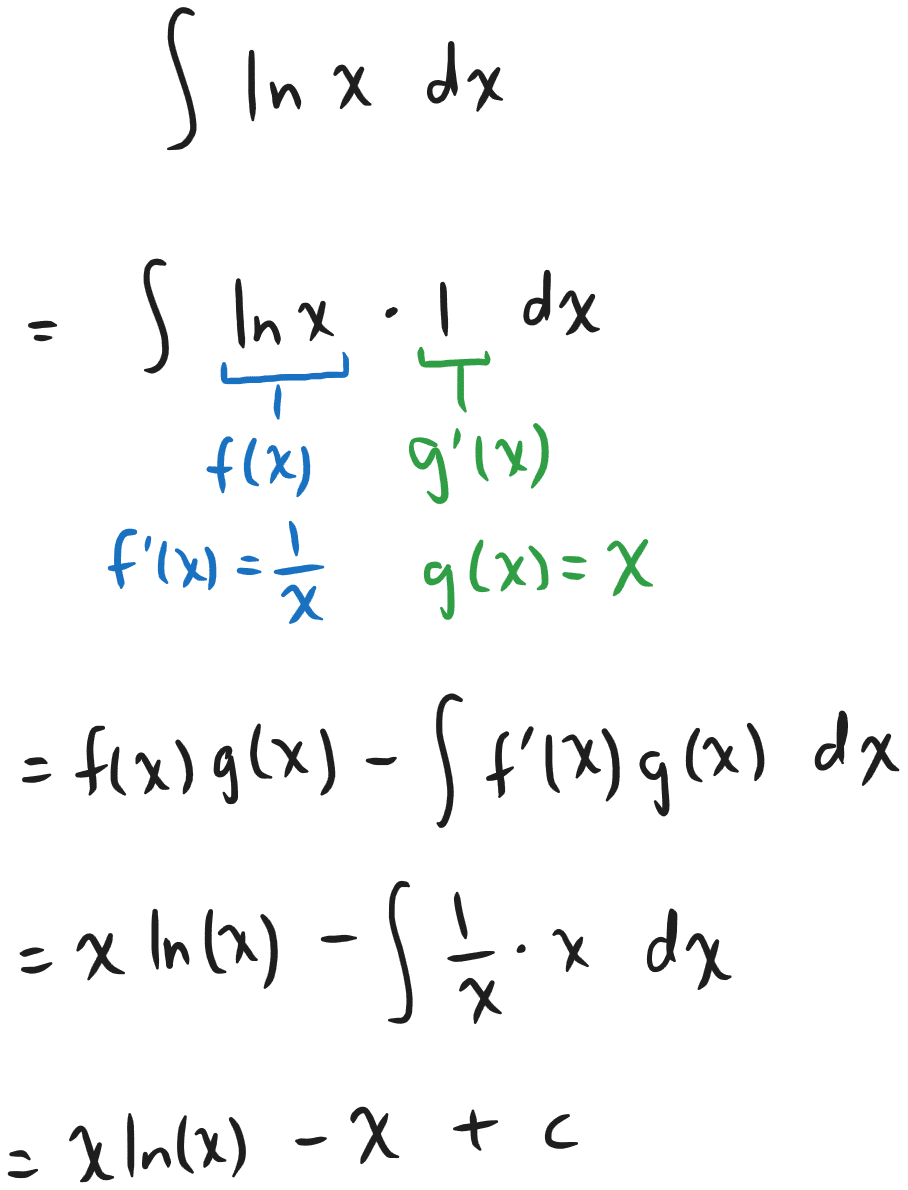
© 2025 James Yap
Personal Website and Knowledge Base
